Tanrı Protokolleri

Bu yazı Nick Szabo’nun 1997'de paylaştığı makalenin Türkçe çevirisidir.

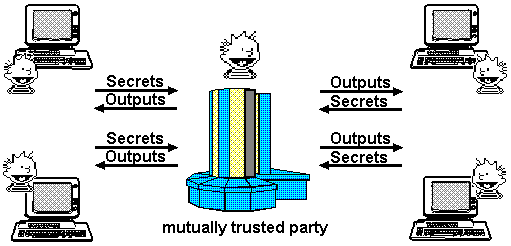
İdeal protokolü hayal edin. Akla gelebilecek en güvenilir üçüncü taraf olurdu, herkesin yanında olan bir tanrı. Bütün partiler girdilerini Tanrı’ya göndereceklerdi. Tanrı sonuçları güvenilir bir şekilde belirleyecek ve çıktıları geri getirecekti. Tanrının itirafı takdirinde en yüce olmak, hiçbir tarafın diğer tarafların girdileri hakkında, kendi girdilerinden ve çıktılarından öğrenebileceklerinden daha fazla bir şey öğrenememesidir.

Ne yazık ki, zamansal dünyamızda tanrılar yerine insanlarla ilgileniyoruz. Ancak, çoğu zaman insanlara neredeyse teolojik olarak davranmak zorunda kalıyoruz, çünkü altyapımız kendimizi korumak için gereken güvenlikten yoksun.

Güvenilir Üçüncü Parti

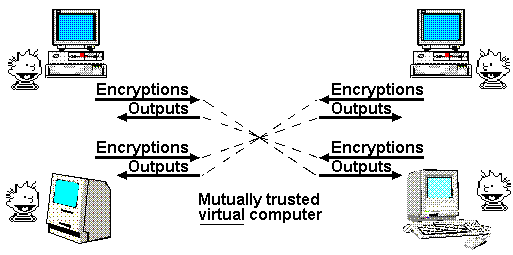
Ağ güvenliği teorisyenleri son zamanlarda bu sorunu şaşırtıcı bir şekilde çözdüler. İki veya daha fazla taraf arasında sanal makineler oluşturan protokoller geliştirdiler. Çok partili güvenli hesaplama, herhangi bir sayıda tarafın bir hesaplamayı paylaşmasına izin verir, her biri yalnızca kendi girdilerinden ve hesaplamanın çıktısından neyin elde edilebileceğini öğrenir. Bu sanal makineler, her bir tarafın girişinin diğer taraflardan kesinlikle gizli tutulması konusunda heyecan verici bir özelliğe sahiptir. Program ve çıktı taraflarca paylaşılmaktadır.

Örneğin, bu sanal bilgisayarda internet üzerinden bir elektronik tablo çalıştırabiliriz. Bir dizi formül üzerinde fikir birliğine varırız ve sanal bilgisayarı bu formüller ile kurarız. Her katılımcının diğer katılımcıların bilgisayarlarında boş kalan, kendi giriş hücrelerine sahip olacaktır. Katılımcılar çıktı hücrelerini paylaşırlar. Kendi özel verilerimizin her bir girdisi kendi girdi hücrelerine girer. Alice sadece diğer katılımcıların girdi hücreleri hakkında, kendi girdilerinden ve çıktı hücrelerinden çıkardığı sonuç kadar çok şey öğrendi.

Matematiksel Güvenilir Protokol

Üç ana sınırlama vardır. İlki, bu sanal bilgisayarın çok yavaş olması: bazı durumlarda, ağ mesajı başına bir aritmetik hesaplama. Şu anda, sadece daha verimli hesaplamalar ve protokollerin tamamlayıcısı veya bileşeni olarak kullanılan küçük mantık veya aritmetik hesaplamalar için en pratik yöntemdir.

İkincisi, gizlilik, adalet ve hata toleransı arasında bir değiş tokuş olduğu. Adalet, herkesin sonuçların hiç kimsenin ilk önce öğrenerek bir avantaj elde etmeyeceği şekilde öğrendiği anlamına gelir. Hata toleransı, azınlığa karşı sağlamlık sağlayabilir ve böylece protokolü durdurmak için çoğunluğun bırakılması gerekebilir ya da tek bir katılımcının protokolü sonlandırabilmesi için zararsız ama durdurma hatası olabilir. Birçok makalede doğru çıktıyı öğrendiğinden emin olmak için güvenilmesi gereken tarafların payı tartışıldı. Geleneksel sonuçlarda, adalet ve gizliliğin her ikisinde de hatalı çoğunluk ile gerçekleşmedi. Son makaleler [3][4][5][6] hatalı çoğunluklarla bile adil ve özel protokoller üretti. Herhangi bir hatalı tarafın oranına karşı gizlilik ve adalet için sağlamlık sağlarlar. Bu kesinti yaklaşımının avantajı, kişinin genellikle yeni ortaklar bulabilmesi ve tekrar başlayabilmesidir, ancak biri sızan bilgi, çantayı tutmaya devam etmek veya yanlış bir sonuçtan ikna olmak gibi geri dönüşü olmayan zararlara maruz kalmak istemez.

Üçüncü sınırlama, her şeyi bilen veya her yerde bulunmaktan uzak, protokolün sadece algoritmada ve girdilerde belirtilenleri gerçekleştirmesidir. Bu, tarafların bilgisayar tarafından sağlanamayan iç görü veya bilgileri sağladığı, insanın güvendiği üçüncü tarafların yerini alamaz.

Bu uyarılarla, herhangi bir algoritmik aracı prensipte, güvenilir bir sanal bilgisayar ile değiştirilebilir. Uygulamada, üç komplikasyon nedeniyle, genellikle daha verimli ögelerden daha sınırlı protokoller inşa ediyoruz.

Çok partili hesaplama teorisinin, özel gizlilik sanal aracılığını mümkün kılarak, teorik olarak her türlü sözleşmeye dayalı ilişki için önemli etkileri vardır. Bu, görüşmeler alanında en net şekilde görülebilir. Ekonomideki bir “mekanizma”, katılımcılarıyla mesaj yoluyla iletişim kuran ve kuralları algoritmik olarak tanımlanabilen soyut bir modeldir. Bu kurumlar açık artırmalar, takaslar, oylamalar vb. olabilir. Genellikle bir tür müzakere veya karar alma sürecini uygularlar.

Ekonomistler, güvenilir bir aracının mekanizması işlettiğini varsayıyorlar. İşte bu sanal bilgisayarı bir mekanizma için kullanmanın basit bir örneği. Alice teklif fiyatını sunabilir, Bob fiyatı sorar sonra bir talimatı olan paylaşılmış sanal programları, “A B’den büyük mü?”. Alice’in teklifi Bob’un teklifinden büyükse, bilgisayar “true” değerini döndürür. Biraz daha sofistike olarak, bilgisayar, uzlaşma fiyatına birkaç farklı algoritmaya göre karar verebilir (Alice’in teklifi, Bob’un sorması, farkı bölmesi vb.) Bu, güvenilir bir aracı olmadan “kör pazarlık” mekanizmasını uygular.

İlke olarak, hesaplanabilir herhangi bir sorun bu sanal bilgisayarda çözülebildiğinden (“Turing tamamlanıyor”), güvenilir bir aracı olmadan herhangi bir hesaplanabilir ekonomik mekanizma uygulanabilir. Uygulamada, yukarıda tartışılan üç sınırlama ile karşı karşıyayız. Ancak, herhangi bir ekonomik mekanizmanın güvenilir bir aracı olmadan çalıştırılabileceğinin kanıtı çok heyecan verici. Bu, ilke olarak, güvenilir bir üçüncü taraf aracılığıyla müzakere edilebilecek herhangi bir sözleşmenin (bir açık artırma veya takas gibi) doğrudan müzakere edilebileceği anlamına gelir. Bu nedenle, bazı soyut anlamda, akıllı sözleşme müzakerelerinde kalan tek “zor” sorun (a) güvenilir bir aracı ile bile zor kabul edilen (standart ekonomik nedenlerle) ve (b) müzakere kurallarını algoritmik olarak belirleme görevidir. ve çıktı sözleşmesi hükümleri (Bu, bir aracının katılımcılara ulaşılamayan bilgileri, örneğin bir sözleşmenin nasıl hazırlanacağına dair tavsiyelerde bulunan bir avukat gibi) eklediği durumları içerir. Uygulamada, protokolleri verimli ve pratik bir şekilde uyguladığımız zaman, prensip olarak çok partili hesaplamayla çözülebilen birçok sorun yeniden ortaya çıkacaktır. Tanrı Protokolleri bize vurmamız için hedef veriyor.

Bu tür bir analizi sözleşmelerin performans aşamasına uygulamak daha az kolaydır. Yeni başlayanlar için, performans aşamasının ekonomik teorileri, müzakere mekanizmaları teorisi kadar gelişmiş veya basit değildir. Aslında, çoğu ekonomik teori, tüm sözleşmelerin kusursuz ve masrafsız bir şekilde uygulanabileceğini varsaymaktadır. “İşlem maliyeti” literatürünün bir kısmı bu varsayımın ötesine geçmeye başlamıştır, ancak sözleşme uygulamalarının teknikleri ve maliyetleri alanında çok az zorlayıcı sonuç veya fikir birliği teorisi vardır.

Çok taraflı güvenli bilgisayar teorisi ile performans aşaması analizi yalnızca sanal bilgisayarın içinde yapılabilecek sözleşmeler için geçerli görünmektedir. Ancak, paylaşılan sanal bilgisayarın içindeki denetim protokollerinin çalıştırılmasıyla bir araya getirildikten sonra, denetlenmeyen denetim günlüklerinin kullanılması, proaktif bir şekilde uygulanmadığı halde, en azından seçilen hakemler tarafından sanal bilgisayarın dışındaki çok çeşitli performansların gözlenip doğrulanmasına izin verir.

Bu karşılıklı gizli denetim protokolüne katılanlar, kitapların daha önce yapılan bir işlem günlüğünde saklanan işlemlerin ayrıntılarıyla eşleştiğini ve sayıların doğru toplandığını doğrulayabilir. Katılımcılar, günlükleri ifşa etmeden günlükleri bir işleme karşı muhataplara karşı kontrol etmek de dahil olmak üzere gizli olarak paylaşılan işlem günlükleri hakkında özet istatistikler hesaplayabilirler. Yalnızca istatistiklerden neyin çıkarılabileceğini öğreniyorlar, işlemlerin ayrıntılarını göremiyorlar. İlginç bir olasılık da, sanal bilgisayarın uzun süre boyunca durumunu koruyabilmesi, karmaşık gizlilik biçimlerine ve kendi kendini uygulayan güvenli krediye izin vermesidir.

Karşılıklı olarak gizli denetim herhangi bir zamanda pratik hale gelirse, karşı tarafların talep ve raporlarının gerçeğine, bu raporların altında yatan işlemlerden tanımlayıcı ve diğer ayrıntılı bilgileri açıklamadan yüksek güven kazanabiliriz. Bunlar, sağlam saygın sistemleri ve zaman içinde bütünlük, iletişim, özetleme ve işlem katılımcıları için gizliliği koruyan diğer güvenilir üçüncü taraf sistemleri için temel sağlayacaktır. Karşılıklı gizli denetimin prensip olarak gerçekleştirilebileceğini bilmek, bu önemli sorunlara pratik çözümler getireceğimizi umut ettiriyor.

Referanslar

1. D. Chaum, C. Crépeau, and I. Damgaard, Multiparty unconditionally secure protocols; In 19th Symp. on Theory of Computing, pages 11–19. ACM, 1988.
2. “The Spymasters Double Agent Problem: Multiparty Computations Secure Unconditionally from Minorities and Cryptographically from Majorities,” D. Chaum, Advances in Cryptology CRYPTO’89, G. Brassard (Ed.), Springer-Verlag, pp. 591–601.
3. C. Crépeau, J. van de Graaf, and A. Tapp, Committed Oblivious Transfer and Private Multi-Party Computations; Advances in Cryptology: Proceedings of Crypto ’95, Springer-Verlag, pages 110–123, 1995. ↩
4. Complete Characterization of Adversaries Tolerable in Secure Multi-Party Computation, Martin Hirt and Ueli Maurer. Computer Science Department, ETH Zürich. 1997. in Proceedings of PODC ’97 ↩
5. Matthias Fitzi, Martin Hirt, and Ueli Maurer: Trading correctness for privacy in unconditional multi-party computation. In Advances in Cryptology — CRYPTO ’98, volume 1462 of Lecture Notes in Computer Science, 1998. ↩
6. R. Cramer, I. Damgaard, S. Dziembowski, M. Hirt, T. Rabin, Efficient Multi-Party Computations with Dishonest Majority, Proceedings of Eurocrypt ’99, Springer Verlag LNCS, to appear (May ‘99). ↩